SciPy 模組

SciPy 模組是一個科學計算模組，專門用來提高數學運算的速度，許多 AI 和機器學習相關的數據分析也需要用到它。下面挑選了幾個和 AI 相關的SciPy 模組~(一樣需要在終端機先安裝，輸入 pip install scipy)

線性代數 scipy.linalg

1. 解聯立線性方程式

SciPy 的 scipy.linalg 主要用來處理線性代數問題，比如解聯立線性方程式。聯立方程式是 AI 和機器學習中處理多變量問題的核心技術之一。

用 scipy.linalg.solve 函數來解兩個變量的聯立方程式，A 是係數矩陣，b 是常數項。

2. 計算行列式 Determinant

行列式在線性代數中非常重要，常用來檢查矩陣是否可逆。而在機器學習中，行列式用來檢查特定變量是否具有唯一解。

用 scipy.linalg.det 函數計算矩陣的行列式，如果行列式不為 0，代表矩陣是可逆的，且方程式有唯一解。

3. 特徵值和特徵向量

在 AI 和機器學習中，特徵值和特徵向量用來簡化資料分析，比如 PCA（主成分分析）用來降維，找出最重要的特徵。

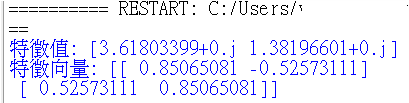
用 scipy.linalg.eig 計算矩陣 A 的特徵值和特徵向量。這些資訊在高維資料降維時，能夠幫助我們了解矩陣的性質。

• eig(A) 函數會返回矩陣 A 的兩個結果：
  eigenvalues：為特徵值，用來表示矩陣在某些線性變換下的行為。
  eigenvectors：為特徵向量，對應於每個特徵值的向量，在矩陣的變換下方向保持不變。

統計 scipy.stats

1. 離散均勻分布 (Uniform discrete distribution)

在AI 中經常需要模擬隨機事件。SciPy 的 scipy.stats 模組可以幫我們生成各種機率分佈。

-randint.rvs(1, 7, size=10)：
這裡是要用來生成範圍內的隨機整數，模擬擲骰子的過程，因為骰子每面上的數字都是隨機的而且出現機率相等。
-參數 (1, 7) 定義數字的範圍（1 到 6），而 size=10 決定了擲骰子的次數。
-.rvs ：
是 SciPy 中的一個方法，來自 randint 函數，全稱是 random variates (隨機變量)。它的功能是從指定的離散分佈或連續分佈中生成隨機樣本。

2. 二項分佈 (Binomial distribution)

二項分佈用來模擬有兩種結果的事件，比如擲硬幣，這樣的操作在機器學習的分類問題中非常重要。

這段程式碼用 scipy.stats.binom.rvs 來模擬多次擲硬幣的結果，呈現了在有兩個可能結果的事件中，SciPy 如何幫助我們做統計。

最佳化 scipy.optimize

解一元二次方程式的根

SciPy 的 optimize 模組幫助我們找到方程的最小值、最大值，或求解非線性方程。

這裡用 scipy.optimize.root 解出一元二次方程式的根，這個方法用來解決非線性問題或優化問題也是很實用的。

小專題：公司銷售統計

一家公司生產兩種產品，每種產品的成本和利潤如下：

• 產品A的成本是 3 美元，利潤是 1 美元。
• 產品B的成本是 1 美元，利潤是 2 美元。

假設公司在某一天的總成本是 9 美元，總利潤是 8 美元，請問他們分別生產了多少產品A和B？

程式碼總覽

解題分析

1. 定義係數矩陣：
   A 是一個 2x2 的矩陣，它代表了聯立方程組的係數。

• 第一個方程式的係數是 3x+1y
• 第二個方程式的係數是 1x+2y

2. 定義常數向量：
   b 是一個向量，表示聯立方程式右邊的常數項，也就是 [9,8]。

• 第一個方程式的常數是 9。
• 第二個方程式的常數是 8。
• 聯立方程式具體表示為：
  3x+y=9
  x+2y=8

3. 解聯立方程式：

• solve(A, b) 是解聯立方程式 A x 𝑥 = b 的方法。
• 這裡的 A 是係數矩陣，b 是常數向量，solve 函數會返回解 x，即產品 A 和產品 B 的生產數量。

4. 輸出結果：最後會顯示聯立方程式的解，也就是公司生產了多少產品 A 和 B。
   

結語

因為之前學過一些基礎的統計，所以 SciPy 的統計模組和最佳化模組讓我很有共鳴。透過 SciPy，我可以更靈活的處理各種分佈問題，像擲骰子、擲硬幣的模擬等。

而透過 root 函數解方程式，也讓我學到了如何用數值方法來找到方程式的解；這跟我們平時學的代數解法很不同，讓我感覺到了程式設計與數學結合後的強大><